数学の勉強法をメールマガジンで紹介しています。
「数学の勉強は頑張っているけど、なぜか成績があがらない」「どうやって勉強をしたらいいか分からない」
そういった人に高校数学をわかりやすく説明しています。
読者さんの声を紹介します。
--------------------------------------------------------------------------------------------
大変役立たせてもらっています。
大昔、塾に通ってた事がありますが、トントン拍子に答えを出して行くだけで、いまいち過程が分からずつまらなかったのを覚えています。
ですから、なぜこうなるか一つ一つ意味を考えることの出来る先生の数学は解いていて分かった時は格別に楽しいです。
-------------------------------------------------------------------------------------------
学校の授業では理屈を教えてくれませんが、どしてこういうことをするのか理由をいちいち説明してくれているからわかりやすいです。問題が解けてもなぜ、何のためにするのか分からないことが多々あります。その理屈を知ることができて数学が楽しくなりました。
-------------------------------------------------------------------------------------------
2010年03月29日
因数定理のプリントを作りました

高校生から上記のような質問を受けました。確かに因数定理って難しいですよね。
でも、この因数定理って簡単に導くことができるんです。
因数定理のプリントを作りましたので、こちらのページをみてください。
因数定理の解説プリント
数学の公式って一見難しそうでも簡単に理解できるものが多いです。ただ単に暗記をするのと理解してから暗記するのとでは大きな差ができます。この因数定理に限らす、どの定理でもそのあたりのことを考えて勉強すると、理解が深まると思います。
それでは、がんばってください。
2010年03月25日
分母に変数がある不等式の解法

上記のような質問を高校生からされました。
方程式や不等式に分数があるときは両辺に適当な数をかけて分数を払ってから解いていくということが基本なんですが、方程式と違って不等式の時は少し注意が必要です。
というのも、不等式の両辺に変数を掛けたら不等号の向きが変わるからです。普通の数だったら間違える人は少ないんですけど、これが文字になると忘れてしまう人が多いです。
両辺に変数を掛けるときは、マイナスの時とプラスの時とで場合わけが必要です。
また数学2の解き方になってしまいますが、場合わけをしないで解く解法もあります。
重要なところですあ、学校で詳しく解説しないところも多いです。解説プリントを作ったので、こちらのページで勉強しておいてください。
分母に変数がある不等式の解法
2010年03月18日
2次関数の重要性
こんにちは、今日は2次関数と指数対数、三角関数の話です。
私は常々「2次関数は、高校数学の関数分野の基礎となるところだから、しっかりと勉強しておくように。2次関数が理解できていたら、そのあとで勉強をする他の関数分野の単元の理解がしやすくなる」というようなことを言い続けています。
そうしたところ、ある高校生から「僕は2次関数は理解できているんですけど、指数対数や三角関数が理解できません。2次関数の知識がどのようにしたら指数対数や三角関数を解くのに役にたつのですか?」といった質問をうけました。
今日は、その疑問に答える形として解説プリントをつくりました。
2次関数と三角関数、指数対数との関係性の解説プリント
上記は、「数学の苦手な人が理解できていないだろうな」というところを中心にかなり詳しく解説しました。1、2年生の人で今現在数学の点をとれてはいるけど、なんとなく解いているという人も多いと思います。
そういった人は、受験が近付くにつれだんだんと点数がとれなくなってきます。上記のプリントは、そういった高校生が見落としやすい点を中心に解説してありますので、もしよければこのプリントで勉強をしてください。
私は常々「2次関数は、高校数学の関数分野の基礎となるところだから、しっかりと勉強しておくように。2次関数が理解できていたら、そのあとで勉強をする他の関数分野の単元の理解がしやすくなる」というようなことを言い続けています。
そうしたところ、ある高校生から「僕は2次関数は理解できているんですけど、指数対数や三角関数が理解できません。2次関数の知識がどのようにしたら指数対数や三角関数を解くのに役にたつのですか?」といった質問をうけました。
今日は、その疑問に答える形として解説プリントをつくりました。
2次関数と三角関数、指数対数との関係性の解説プリント
上記は、「数学の苦手な人が理解できていないだろうな」というところを中心にかなり詳しく解説しました。1、2年生の人で今現在数学の点をとれてはいるけど、なんとなく解いているという人も多いと思います。
そういった人は、受験が近付くにつれだんだんと点数がとれなくなってきます。上記のプリントは、そういった高校生が見落としやすい点を中心に解説してありますので、もしよければこのプリントで勉強をしてください。
2010年03月18日
菜の花のパスタを作りました
こんにちには
「最近パスタ作りにはまっている」と友達にいったところ、フライパンをもらいました。
さっそく、そのフライパンで「菜の花のパスタ」を作りました。
小さいころは、どうでもよかったんですが最近は菜の花なんて季節を感じる食材が好きになりました。そういや、最近はテレビ東京の旅番組を良く見ています。

「最近パスタ作りにはまっている」と友達にいったところ、フライパンをもらいました。
さっそく、そのフライパンで「菜の花のパスタ」を作りました。
小さいころは、どうでもよかったんですが最近は菜の花なんて季節を感じる食材が好きになりました。そういや、最近はテレビ東京の旅番組を良く見ています。

Posted by 河見賢司 at
08:45
│Comments(0)
2010年03月17日
積分の面積の考え方
こんにちは
積分の面積の意味って知っていますか?よく公式として理解している人が多いですが、積分の意味を理解したら公式なんて必要なくなりますよ。
積分の意味は、「微小区間を足し合わせて全体を作る」です。微小区間なんて聞くと難しそうですが、実際は小学生でも理解できるような簡単な内容なんですよ。
進学校でさえ教えてくれないというところもあります。本当に簡単に理解できるので積分の面積の意味を解説したプリントを作りました。
積分の公式の意味の解説プリント
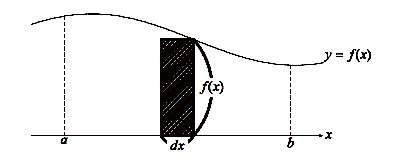
積分の面積の意味って知っていますか?よく公式として理解している人が多いですが、積分の意味を理解したら公式なんて必要なくなりますよ。
積分の意味は、「微小区間を足し合わせて全体を作る」です。微小区間なんて聞くと難しそうですが、実際は小学生でも理解できるような簡単な内容なんですよ。
進学校でさえ教えてくれないというところもあります。本当に簡単に理解できるので積分の面積の意味を解説したプリントを作りました。
積分の公式の意味の解説プリント
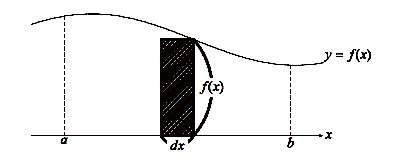
2010年03月09日
相加相乗平均の使い方
こんにちは、高校生から以下のような質問を受けました。

確かにどういったときに相加相乗平均を使うのか気付きにくいと思います。相加相乗平均って、正という条件が与えられていて、和の形になっているとこ互いにかけあわせたとき変数(文字)が消えてくれるときに相加相乗平均を使います。
少しブログでは説明しにくいので、解説プリントを作りました。
相加相乗平均の使い方
相加相乗平均って学校では適当にしか勉強をしないところが多いですが、大学受験には頻出なんです。相加相乗平均って何?というくらいの人もいますが、相加相乗平均をしっかりと勉強するようにしてください。
それでは、がんばってください。

確かにどういったときに相加相乗平均を使うのか気付きにくいと思います。相加相乗平均って、正という条件が与えられていて、和の形になっているとこ互いにかけあわせたとき変数(文字)が消えてくれるときに相加相乗平均を使います。
少しブログでは説明しにくいので、解説プリントを作りました。
相加相乗平均の使い方
相加相乗平均って学校では適当にしか勉強をしないところが多いですが、大学受験には頻出なんです。相加相乗平均って何?というくらいの人もいますが、相加相乗平均をしっかりと勉強するようにしてください。
それでは、がんばってください。
2010年03月06日
指数・対数の桁数に関するプリントを作りました
こんにちは
突然なんですが、桁数にかんする問題をしっかりと理解していますか?桁数に関する問題というのは、たとえば「2の20乗は何桁の整数になるか?」といった問題です。
この問題なんですが、適当にしか理解していない人も多いです。意味もわからずになんとなくlogをつけて解いてるという人も多いと思います。
こんなこと言っていますが、僕も高校生の時は意味も分からずに解いていました(笑)
でも、これって簡単に意味を理解することができるんです。ブログでは少し解説しにくいので、解説プリントを作りました。
もしよければ、こちらの解説プリントで勉強してください。
桁数に関する解説プリント
突然なんですが、桁数にかんする問題をしっかりと理解していますか?桁数に関する問題というのは、たとえば「2の20乗は何桁の整数になるか?」といった問題です。
この問題なんですが、適当にしか理解していない人も多いです。意味もわからずになんとなくlogをつけて解いてるという人も多いと思います。
こんなこと言っていますが、僕も高校生の時は意味も分からずに解いていました(笑)
でも、これって簡単に意味を理解することができるんです。ブログでは少し解説しにくいので、解説プリントを作りました。
もしよければ、こちらの解説プリントで勉強してください。
桁数に関する解説プリント
2010年03月03日
三角形の面積:ヘロンの公式
こんにちは
突然なんですが、ヘロンの公式って知っていますか?ヘロンの公式は、三角形の面積を求める公式ですが、三角形で3辺の長さが整数で与えられている時にこのヘロンの公式を使うと簡単に求めることができます。
ヘロンの公式自体は知っている人も多いとは思いますが、ヘロンの公式を証明できる人は少ないです。
公式の証明は計算が難しかったり、計算法がなかなか思いつかないというものが多いです。このヘロンの公式も難しく、なかなか自分では導けないと思います。
教科書や問題集でヘロンの公式を証明しているものもありますが、「なぜそこでそのような式変形をしたのか」ということが書かれていないことが多く、一人では分かりにくかったと思います。
そこで、今回はヘロンの公式の証明を「なぜそこでそのような式変形をしたのか」ということをかなり詳しく解説したプリントを作りました。
ヘロンの公式の証明
解答はかなり詳しく書いたので、ぜひともこのプリントを参考にしてください。
突然なんですが、ヘロンの公式って知っていますか?ヘロンの公式は、三角形の面積を求める公式ですが、三角形で3辺の長さが整数で与えられている時にこのヘロンの公式を使うと簡単に求めることができます。
ヘロンの公式自体は知っている人も多いとは思いますが、ヘロンの公式を証明できる人は少ないです。
公式の証明は計算が難しかったり、計算法がなかなか思いつかないというものが多いです。このヘロンの公式も難しく、なかなか自分では導けないと思います。
教科書や問題集でヘロンの公式を証明しているものもありますが、「なぜそこでそのような式変形をしたのか」ということが書かれていないことが多く、一人では分かりにくかったと思います。
そこで、今回はヘロンの公式の証明を「なぜそこでそのような式変形をしたのか」ということをかなり詳しく解説したプリントを作りました。
ヘロンの公式の証明
解答はかなり詳しく書いたので、ぜひともこのプリントを参考にしてください。








